Webサイトはグラフ構造で捉えよ。ツリー構造の数学的脆弱性と固有ベクトル中心性による証明

はじめに:Webサイトを「グラフ」として再定義する
多くのWebサイト運営者が、無意識のうちにサイト構造を「フォルダ分け」のような階層、すなわち「ツリー構造」として捉えています。それは直感的で分かりやすい一方、現代の検索エンジンが世界を認識する方法とは、もはや乖離が生じているかもしれません。本記事では、その固定観念を一度リセットし、Webサイトをページ(ノード)とリンク(エッジ)から成る広大な「有向グラフ」として再定義することから始めます。
この視点の転換は、単なる言葉遊びではありません。AIがウェブの文脈を深く理解しようとする現代において、サイトの真の価値を評価するための根源的なアプローチなのです。事実、Googleの検索順位を決定づける最も有名なアルゴリズムの一つであるPageRankは、Webリンクを確率遷移として正規化した行列にランダムジャンプ(ダンピング)を組み込んだ「Google行列」の定常分布(固有値1に対応する固有ベクトル)として定式化されます※1。これは、Webサイトの構造が持つ数学的な特性こそが、その評価を本質的に決定づけていることの何よりの証左と言えるでしょう。
この記事では、なぜ従来のツリー構造が数学的な脆弱性を抱えているのか、そして密な結合を持つグラフ(メッシュ)構造がいかにしてその評価を最大化するのかを、線形代数とグラフ理論を用いて論理的に証明していきます。感覚論ではない、数理に基づいたサイト設計の本質に迫っていきましょう。このテーマの全体像については、AI時代の新サイト設計論『セマンティック・メッシュ・バイパスモデル』の全貌で体系的に解説しています。
※1.Google行列とPageRankの数学的定義については、スタンフォード大学の原典論文「The PageRank Citation Ranking: Bringing Order to the Web」の定義(2.1項)を参照。
ツリー構造の数学的脆弱性:なぜ階層型サイトは評価が拡散しないのか
従来のWebサイト設計で主流であったツリー構造(階層型・サイロ型)は、一見すると整理されていて管理しやすいように思えます。しかし、その構造はSEOにおいて、評価をサイト全体に行き渡らせる上で構造的な限界を抱えています。ここでは、その限界をグラフ理論と線形代数を用いて数学的に証明していきます。「感覚的に知っていた問題」の背後にある、揺るぎない数理的な裏付けを明らかにしていきましょう。
サイト構造の線形代数的表現:隣接行列とは何か
Webサイトのリンク構造を数学的に扱うための第一歩は、それを「隣接行列(Adjacency Matrix)」に変換することです。隣接行列とは、グラフのノード間の接続関係を行列で表現したもので、Webサイトにおいてはサイトのトポロジー(位相幾何学的な構造)を完全に表現する「設計図」の役割を果たします。
サイトにN個のページが存在する場合、隣接行列AはN×Nの正方行列となります。行列の各要素 Aij は、以下のように定義されます。
- Aij = 1:ページiからページjへのリンクが存在する場合
- Aij = 0:ページiからページjへのリンクが存在しない場合
例えば、5つのページからなる単純なツリー構造とメッシュ構造を考えてみましょう。
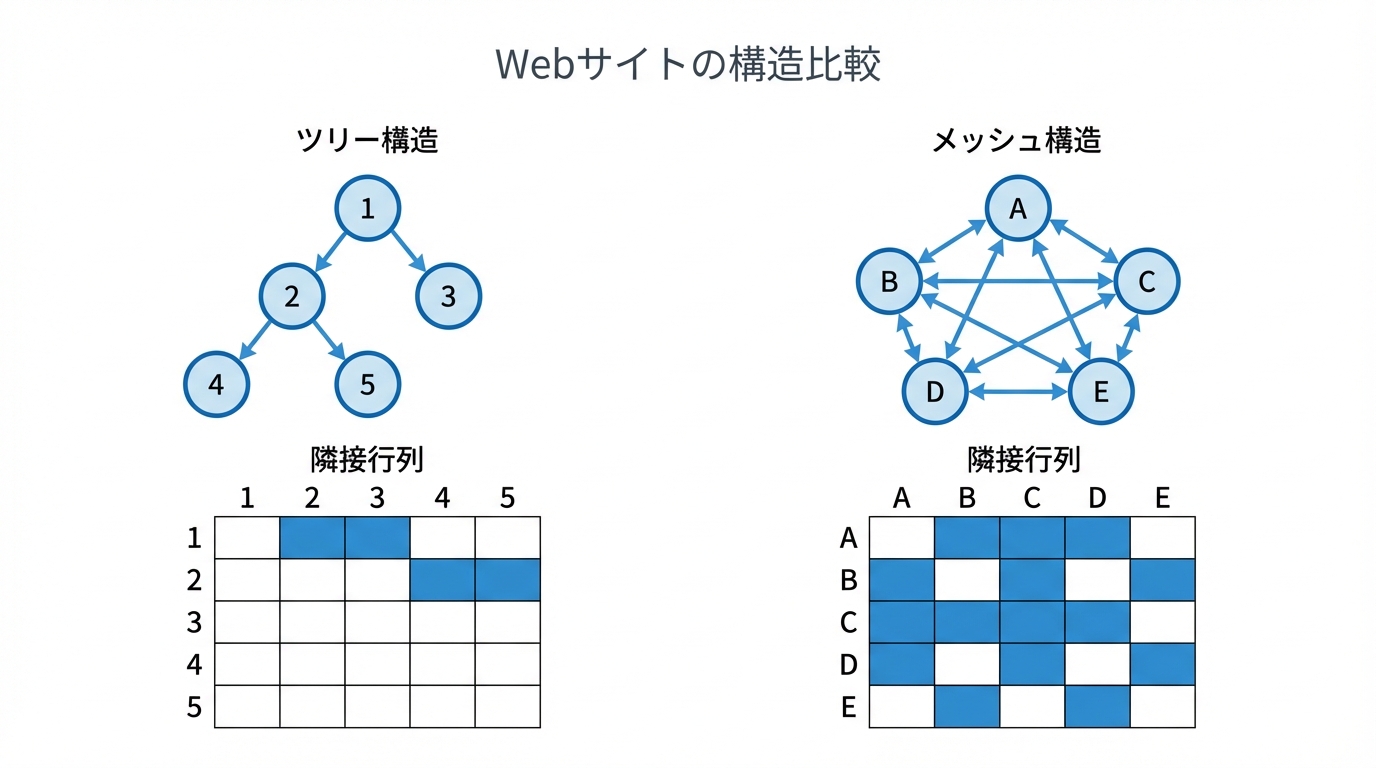
ツリー構造では、リンクはトップページから下層へ一方向に流れるだけです。一方、メッシュ構造では、下層のページ間にも相互リンクが存在します。この違いは、それぞれの隣接行列に明確に現れます。ツリー構造の隣接行列は成分のほとんどが0(疎行列)になるのに対し、メッシュ構造の隣接行列は1の成分が多くなります。この行列の「形」の違いこそが、後述する評価の伝播効率を決定づけるのです。
固有ベクトル中心性による「重要度」の計算メカニズム
GoogleのPageRankは、「固有ベクトル中心性(Eigenvector Centrality)」の考え方をベースにしつつ、リンクの正規化やランダンピング(ランダムジャンプ)を加えて安定に計算できるようにした派生手法の一つです。この概念の核心は、「重要なページからリンクされているページは、同様に重要である」という再帰的な定義にあります。
あるページjの重要度スコアを xj とすると、この定義は以下の数式で表現できます。
xj = (1/λ) * Σi Aji * xi
ここで、Aji は隣接行列の成分、λは定数(固有値)です。これを行列形式で書くと、非常にシンプルな形になります。
Gx = x
これは線形代数における固有値問題(固有値1)です。つまり、ページの重要度スコアのベクトル x は、リンクを出リンクで正規化した遷移行列にランダムジャンプ(ダンピング)を組み込んだGoogle行列 G の固有ベクトル(定常分布)として求められます。
この固有ベクトルを求めるためのアルゴリズムの一つが「冪乗法(Power Iteration)」です。これは、任意の初期ベクトル v0 に隣接行列 A を繰り返し乗算していくことで、最大固有値に対応する固有ベクトルに収束させる手法です。
vk+1 = A vk / ||A vk||
この計算プロセスは、「リンクを1回たどる」操作を数学的に表現しています。行列を掛けるたびに、各ページが持つスコアがリンクを通じて隣のページへと分配されていくのです。この計算を繰り返すことで、最終的にサイト全体の安定したスコア分布、すなわち固有ベクトル中心性が明らかになります。それは、単に被リンク数が多いだけでなく、サイト構造全体の中でどのページがハブとして機能しているかを反映した、より本質的な網羅的な評価指標となります。
証明:ツリー構造が中心性を末端に伝播できない数学的理由
いよいよ本題です。なぜツリー構造は評価を末端ページに効率的に伝えられないのでしょうか。その答えは、ツリー構造の隣接行列に冪乗法を適用した際のスコアの振る舞いにあります。
ツリー構造の最大の特徴は、リンクが一方向に分岐するだけで、決して合流しない(ループが存在しない)点にあります。これを隣接行列の言葉で表現すると、行列を何乗かすると必ず零行列(すべての成分が0の行列)になる「冪零性」に近い性質を持ちます。
冪乗法の計算過程(vk+1 = A vk)において、トップページに初期集中したスコアは、リンクをたどる(行列Aを掛ける)たびに下層ページへと分配されます。しかし、ツリー構造ではリンクが一方通行であるため、一度下層に渡されたスコアが再び上層や他のブランチ(枝)に戻ることはありません。スコアは下へ下へと流れるだけで、まるで滝のようにエネルギーを失いながら拡散していきます。
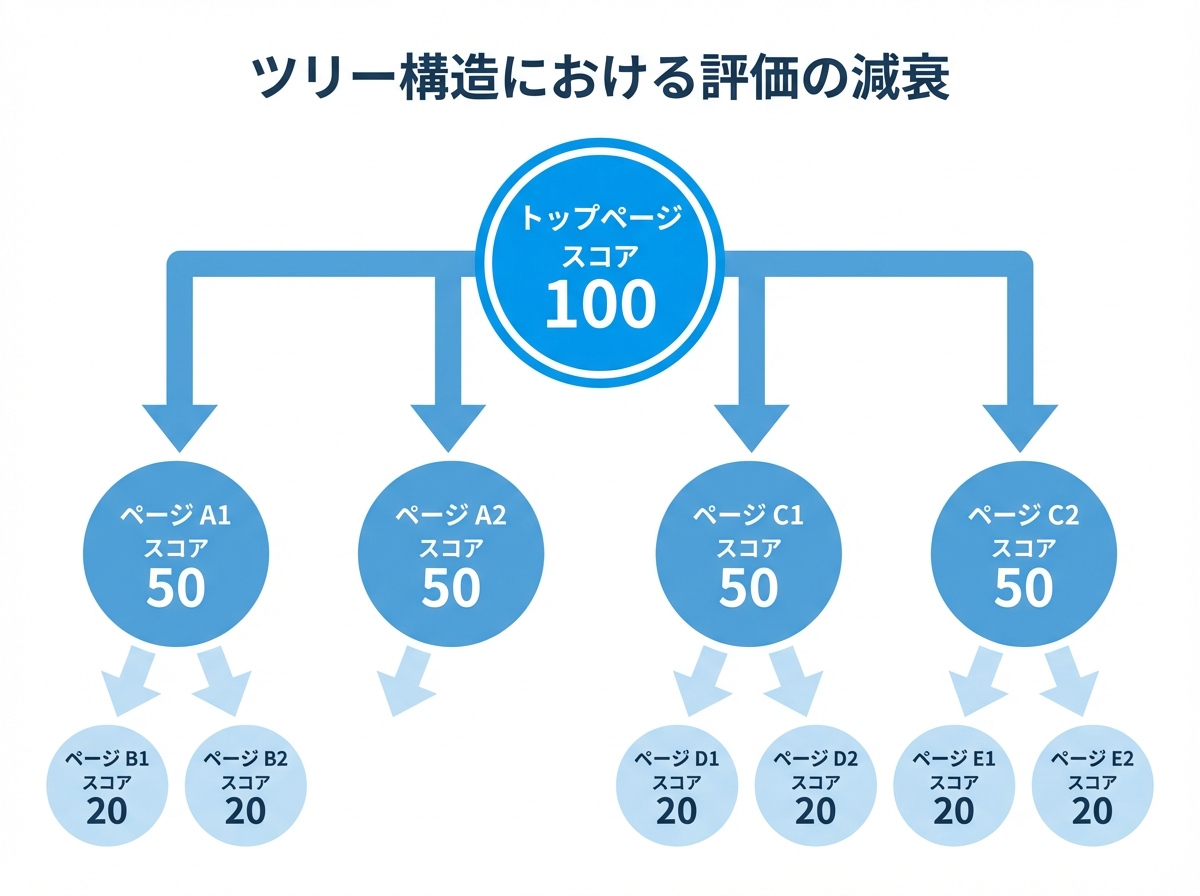
その結果、トップページから遠い末端ページ(クロール深度が深いページ)に到達するスコアは、指数関数的に減衰してしまいます。さらに深刻なのは、異なるカテゴリ(ブランチ)に属する末端ページ同士は、グラフ上で非常に「遠い」存在であるという事実です。共通の祖先ノードまで何ステップも遡らなければならず、互いにスコアを与え合う経路が存在しません。これにより、サイト全体でスコアを還流させることができず、中心性の総和が低く抑えられてしまうのです。
これこそが、SEOで言われる「情報のサイロ化」や「クロール深度の問題」の数学的な本質です。厳格なカテゴリ設計が、逆にページ間の連携を断絶させ、サイト全体のポテンシャルを削いでしまうという構造的欠陥が、隣接行列の性質から明確に証明されるのです。この構造は、限定的なトピッククラスター戦略においても同様の課題を内包しています。
グラフ構造の数学的優位性:密な結合が中心性を最大化する証明
前章でツリー構造の数学的脆弱性を論証しました。では、その解決策となるグラフ(メッシュ)構造は、なぜ数学的に優れているのでしょうか。ここでは、メッシュ構造がもたらす特性をグラフ理論の指標で解き明かし、中心性スコアがサイト全体に広がりやすくなるメカニズムを、数理モデル上の前提を置いたうえで論証します。
スモールワールド性の実現:平均経路長とクラスター係数
密な内部リンクで構築されたメッシュ構造は、「スモールワールド性」という非常に重要な特性を獲得します。これは、私たちの実社会の人間関係にも見られるネットワークの性質で、以下の2つの指標によって特徴づけられます。
- 平均経路長(Average Path Length)の短さ
サイト内の任意の2ページ間を移動する際の最短リンク数(クリック数)の平均値です。メッシュ構造では、関連ページ同士が直接リンクで結ばれるため、ツリー構造のように一度上位階層に戻る必要がありません。これにより、平均経路長は劇的に短縮されます。これは、ユーザーが必要な情報へ素早くたどり着ける高い回遊性を意味し、同時にGoogleのクローラーがサイト全体を効率的に巡回できる(クロールバジェットを有効活用できる)ことを示唆します。 - クラスター係数(Clustering Coefficient)の高さ
あるページの隣接ページ同士が、互いにリンクし合っている度合いを示す指標です。クラスター係数が高いということは、局所的に密なリンクのコミュニティ(クラスター)が形成されていることを意味します。
これは、特定のトピックに関連するページ群が強く結束している状態を指します。つまり、無秩序にリンクを張り巡らせるのではなく、意味のあるトピックの塊ごとに密なネットワークを作るという、本モデルの重要な概念『半透膜』が数学的にも正しい状態であることを裏付けています。
この高いクラスター係数は、ユーザーの回遊性を高めると同時に、検索エンジンがサイト内のトピックの関連性を正確に把握するうえで、極めて有利に働きます。
ツリー構造では、平均経路長は長く、クラスター係数はほぼゼロに近くなります。対照的に、メッシュ構造はこれら両方の指標を劇的に改善し、ユーザーと検索エンジンの双方にとって「見通しの良い」理想的なネットワークを構築するのです。
証明:メッシュ構造が固有ベクトル中心性を全体に還流させる仕組み
メッシュ構造の数学的優位性は、その隣接行列に冪乗法を適用した際のスコア伝播プロセスを分析することで、より明確に証明できます。
ツリー構造との決定的な違いは、「ループ(閉路)」の存在です。メッシュ構造では、末端ページ同士が相互にリンクを持つことで、スコアが循環する経路が無数に生まれます。冪乗法の計算過程において、あるページから分配されたスコアは、他のページを経由して再び自身に戻ってくることが可能になります。この「スコアの還流」こそが、中心性を最大化する鍵です。
数学的には、隣接行列内にループが存在すると、行列を累乗しても成分が0になりにくくなります。スコアは系(システム)の外に散逸することなく、サイト内部を循環し続けます。この還流効果は、ネットワークが強連結に近づき、冪乗法で求める中心性(定常分布)がサイト全体に行き渡りやすくなる方向に働きます。結果として、特定のページにスコアが極端に偏りにくくなり、より多くのページが一定の中心性を持つ分布になりやすいのです。
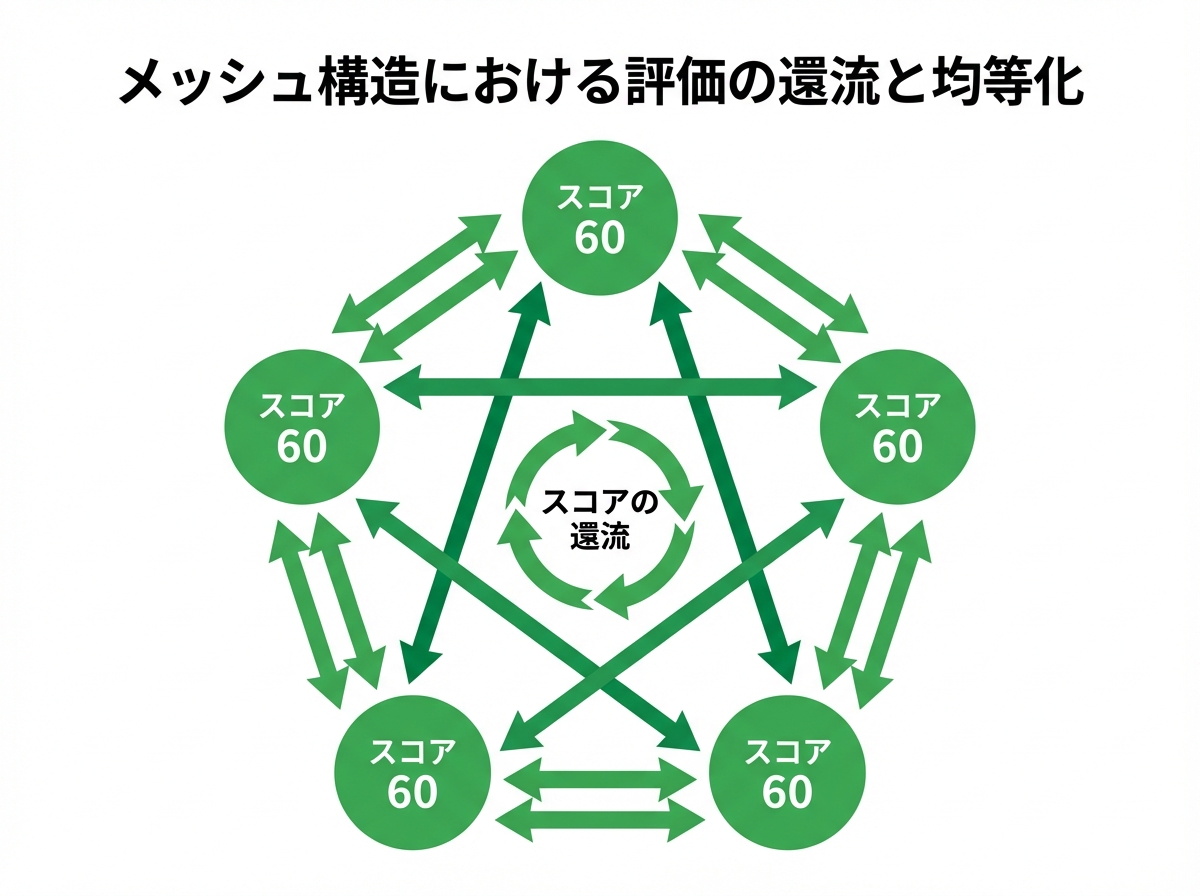
シミュレーションを行うと、その差は一目瞭然です。同じページ数、同じ総リンク数であっても、ツリー構造ではトップページとごく一部の上位ページにスコアが偏在し、末端はほぼゼロに近い値になります。一方、メッシュ構造では、スコアがサイト全体に広く分配され、どのページも一定以上の中心性を保持するようになります。これは、個々の記事が持つ価値を余すことなくサイト全体の評価へと繋げ、ロングテール記事の活躍を促す理想的な状態と言えるでしょう。
結論:数学的観点から有力なサイト構造『セマンティック・メッシュ・バイパスモデル』
これまでの数学的な論証を総括すると、Webサイトの評価を最大化するための構造的最適解が見えてきます。それは、私たちが提唱する『セマンティック・メッシュ・バイパスモデル』です。
このモデルは、単なるツリー構造でも、無秩序なメッシュ構造でもありません。ツリー構造(バイパスによる階層性)が持つ「権威の戦略的集中」というメリットと、メッシュ構造が持つ「評価の分散と還流」というメリットを両立させる、ハイブリッドな最適解なのです。
- セマンティック・メッシュ:AIがコンテンツの「意味」を理解し、関連性の高いページ同士を網の目のように自律的に接続します。これにより、サイト全体のスモールワールド性が担保され、固有ベクトル中心性が効率的に還流する土台が築かれます。
- 戦略的バイパス:人間がビジネス上の重要度を判断し、収益に直結するページや、テーマの核となるピラーページへのリンク(バイパス)を戦略的に設置します。これにより、還流する中心性を意図した場所へと誘導し、ビジネスゴール達成を加速させます。
AIによる意味的接続がサイト全体の地力を高め、人間による戦略的リンクがその力をビジネス成果へと結びつける。この二つの要素が組み合わさることで、サイト全体の評価が高まりやすい構造を、数学的観点から狙うことができます。このモデルの全体像については、AI時代の新サイト設計論『セマンティック・メッシュ・バイパスモデル』の全貌で詳しく解説していますので、併せてご覧ください。
理論を実装するエンジン:OGAIによるメッシュ構造の自律構築
本記事で展開した高度なグラフ理論を、現実のサイト運用に落とし込むにはどうすればよいのでしょうか。数千、数万ページに及ぶサイトで、意味的に関連するページを見つけ出し、最適なメッシュ構造を人力で構築・維持することは、もはや不可能です。
セマンティック・メッシュ構造の構築には、全コンテンツの意味的関連性を大規模かつ動的に把握し、最適なリンクを自律的に生成する高度な技術が不可欠です。そして、私たちが開発したセマンティック・メッシュ・バイパスモデル対応のAIライティングツール「OGAI」は、まさにこの理論を実装するために生まれたエンジンです。
OGAIは、サイト内の全コンテンツをベクトル表現で解析し、意味的に近いページ同士を自動で検知・接続します。これにより、人間では到底不可能な規模と精度で、数学的に最適化されたセマンティック・メッシュを自律的に構築・維持します。これまで解説してきた理論の正しさを現実世界で具現化し、サイトのポテンシャルを最大限に引き出す。それがOGAIの提供するソリューションなのです。

